2.1.1. Supercontinuum generation in a PCF

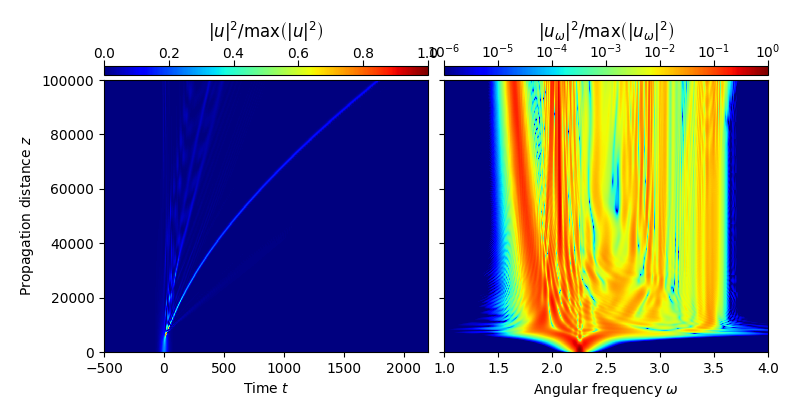
This examples demonstrates the \(z\)-propagation of a specialized propagation model for a specific propagation constant, implemented using the simplified forward model for the analytis signal including the Raman effect.

The propagation scenario schown below, is discussed on several occations in the scientific literature [1-3]. For example, in Ref. [1], it is used to demonstrate numerical simulations in terms of the gneralized nonlinear Schrödinger equation (GNSE) on supercontinuum generation for an instance of a highly nonlinear photonic crystal fiber (PCF) with an anomalous group-velocity dispersion regime. In Ref. [2] it is used, again using the GNSE, to introduce a particular \(z\)-propagation algorithm referred to as the “Runge-Kutta in the interacton picture” (RK4IP) method. This algorithm, a particular variant of an integrating-factor method, is also implemented in py-fmas. In Ref. [3] it is used to demonstrate the feasibility of an adaptive step-size method for the simulation of supercontinuum generation in optical fiber.

All the above simulation studies used the generalized nonlinear Schrödinger equation wich relies on the slowly varying envelope approximation. In contrast to this, the below example employs a non-envelope model, namely by the simplified forward model for the analytic signal with added Raman effect (FMAS-S-R) [4-6]. The \(z\)-propagation algorithm used with the FMAS-S-R in conjunction with the RK4IP method.

References:

[1] J. M. Dudley, G. Genty, S. Coen, Supercontinuum generation in photonic crystal fiber, Rev. Mod. Phys. 78 (2006) 1135, http://dx.doi.org/10.1103/RevModPhys.78.1135

[2] J. Hult, A Fourth-Order Runge–Kutta in the Inter- action Picture Method for Simulating Supercontin- uum Generation in Optical Fibers, IEEE J. Light- wave Tech. 25 (2007) 3770, https://doi.org/10.1109/JLT.2007.909373.

[3] A. M. Heidt, Efficient Adaptive Step Size Method for the Simulation of Supercontinuum Generation in Optical Fibers, IEEE J. Lightwave Tech. 27 (2009) 3984, https://doi.org/10.1109/JLT.2009.2021538

[4] Sh. Amiranashvili, A. Demircan, Hamiltonian structure of propagation equations for ultrashort optical pulses, Phys. Rev. E 10 (2010) 013812, http://dx.doi.org/10.1103/PhysRevA.82.013812.

[5] Sh. Amiranashvili, A. Demircan, Ultrashort Optical Pulse Propagation in terms of Analytic Signal, Adv. Opt. Tech. 2011 (2011) 989515, http://dx.doi.org/10.1155/2011/989515.

[6] A. Demircan, Sh. Amiranashvili, C. Bree, C. Mahnke, F. Mitschke, G. Steinmeyer, Rogue wave formation by accelerated solitons at an optical event horizon, Appl. Phys. B 115 (2014) 343, http://dx.doi.org/10.1007/s00340-013-5609-9

import fmas
import numpy as np
from fmas.models import CustomModelPCF
from fmas.solver import IFM_RK4IP
from fmas.analytic_signal import AS
from fmas.grid import Grid
from fmas.tools import plot_evolution


def main():
    # -- DEFINE SIMULATION PARAMETERS
    # ... COMPUTATIONAL DOMAIN
    t_max = 3500.       # (fs)
    t_num = 2**14       # (-)
    z_max = 0.10*1e6    # (micron)
    z_num = 8000        # (-)
    z_skip = 10         # (-)
    # ... INITIAL CONDITION
    P0 = 1e4            # (W)
    t0 = 28.4           # (fs)
    w0 = 2.2559         # (rad/fs)
    E_0t_fun = lambda t: np.real(np.sqrt(P0)/np.cosh(t/t0)*np.exp(-1j*w0*t))

    # -- INITIALIZATION STAGE
    # ... COMPUTATIONAL DOMAIN
    grid = Grid( t_max = t_max, t_num = t_num, z_max = z_max, z_num = z_num)
    # ... CUSTOM PROPAGATION MODEL
    model = CustomModelPCF(w=grid.w)
    # ... PROPAGATION ALGORITHM
    solver = IFM_RK4IP( model.Lw, model.Nw, user_action = model.claw)
    solver.set_initial_condition( grid.w, AS(E_0t_fun(grid.t)).w_rep)

    # -- RUN SIMULATION
    solver.propagate( z_range = z_max, n_steps = z_num, n_skip = z_skip)

    # -- SHOW RESULTS
    plot_evolution( solver.z, grid.t, solver.utz,
        t_lim = (-500,2200), w_lim = (1.,4.))


if __name__=='__main__':
    main()